Understanding Fractions

Recap: A fraction consists of a numerator (representing the part) and a denominator (representing the whole).

Adding Fractions with the Same Denominator

Let's revisit adding fractions with the same denominator, illustrated with 1/5 + 3/5.

1. Same Denominator: Both fractions have the same denominator of 5.
2. Add the Numerators: (1 + 3)/5 = 4/5.

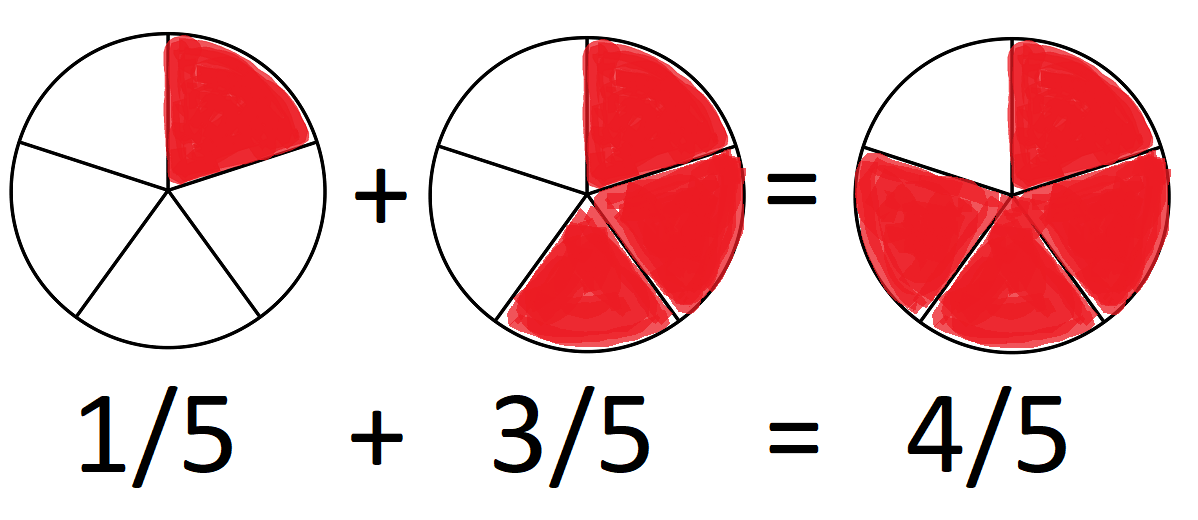
Simplify (if possible): 4/5 is alread simplified. Thus, 1/5 + 3/5 = 4/5.

Adding and Subtracting Fractions with Different Denominators

Method 1: Cross-Multiplication

Consider 1/3 + 1/6 and 4/5 - 2/5.

Adding Fractions

1. Cross-Multiply to Find a Common Denominator: 3 × 6 = 18.
2. Adjust the Fractions: Convert 1/3 to 6/18 and 1/6 to 3/18.
3. Add the Numerators: 6/18 + 3/18 = 9/18.
4. Simplify (if possible): 9/18 = 1/2.

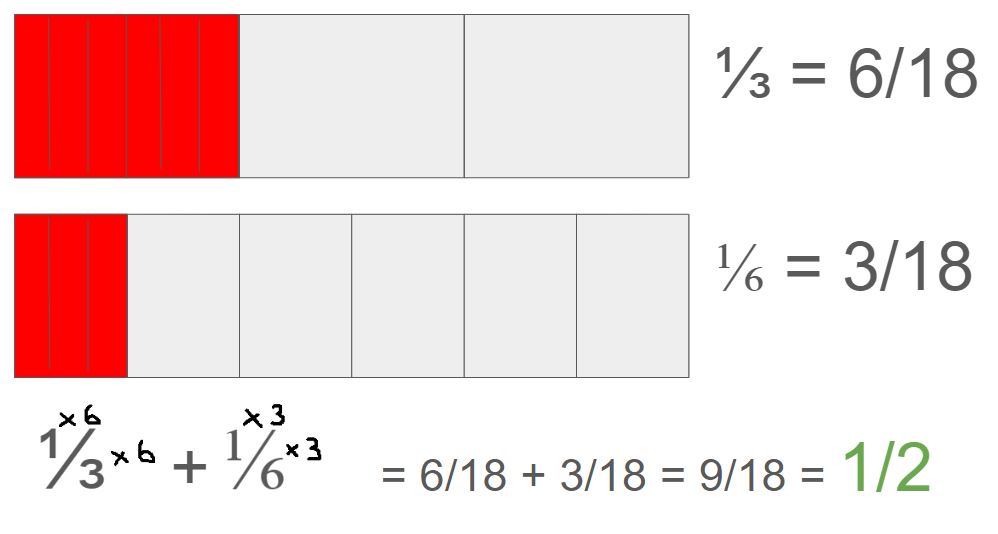
Simplify (if needed): 3/6 simplifies to 1/2. Thus, 1/3 + 1/6 = 1/2.

Subtracting Fractions

1. Cross-Multiply to Find a Common Denominator: 5 × 5 = 25.
2. Adjust the Fractions: No adjustment needed as denominators are already the same.
3. Subtract the Numerators: (4 - 2)/5 = 2/5.

Simplify (if needed): 2/5 is already simplified.

Method 2: Using Lowest Common Multiple (LCM)

Consider 1/3 + 1/6 and 4/5 - 2/5.

Adding Fractions

1. Find LCM: LCM of 3 and 6 is 6.
2. Adjust the Fractions: Convert 1/3 to 2/6.
3. Add the Numerators: 2/6 + 1/6 = 3/6.

Simplify (if needed): 3/6 simplifies to 1/2. Thus, 1/3 + 1/6 = 1/2.

Subtracting Fractions

1. Find LCM: LCM of 5 and 5 is 5.
2. Adjust the Fractions: No adjustment needed as denominators are already the same.
3. Subtract the Numerators: (4 - 2)/5 = 2/5.

Simplify (if needed): 2/5 is already simplified.

Conclusion

You've now explored two methods for adding and subtracting fractions with different denominators: cross-multiplication and using the lowest common multiple. Practice with various examples to reinforce your skills. Keep enjoying your journey through GCSE Mathematics!